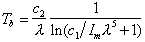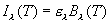
where e_l is the emissivity of the object, which varies between 0 and 1. If e_l does not depend on wavelength we say that the object is a gray body; a blackbody has a value of e_l=1.

How are emission and absorption related? Imagine an object that absorbs perfectly at one wavelength but not at all at any other wavelength (that is, an object with e_l=1 at one value of 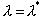and e_l= 0 everywhere else), illuminated by broadband blackbody radiation from a second body. The object absorbs the incident radiation and warms; as it warms the emission (which occurs only at l^?, remember) increases. Equilibrium is reached when the amount of energy emitted by the particle E_out is equal to the amount absorbed E_in. At wavelength l^? the body acts as a blackbody, so emission depends only on the equilibrium temperature and 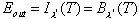. The body is exposed to broadband blackbody radiation, so 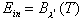. But since equilibrium implies that 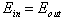, the absorption at every wavelength other than l^*must be zero. This chain of reasoning, known as Kirchoff’s Law, tells us that the absorptivity and emissivity of objects is the same at every wavelength.

The Planck function finds another application in the computation of brightness temperature. If we make measurements of monochromatic intensity I_m at some wavelength l, and assume that e_l =1, we can invert the Plank function to find the temperature T_b at which a blackbody would have to be in order to produce the measured intensity

T_b is called the equivalent blackbody temperature or, more commonly, brightness temperature. It provides a more physically recognizable way to describe intensity.

Back

Return to Lesson 2
Return to Satellite Meteorology Main Page